0. 引言：语言模型任务的数学定义

自然语言可以看作是由有限词表 $\mathcal{V}$ 生成的离散序列

$$x_1, x_2, \dots, x_T,\quad x_t \in \mathcal{V}.$$

语言模型（Language Model, LM）的目标是构建一个概率分布：

$$p(x_1,\dots,x_T)=\prod_{t=1}^{T} p(x_t \mid x_{<t}),$$

其中 $x_{<t}=x_1,\dots,x_{t-1}$。

也就是说，模型需要学会在给定前缀的情况下，为下一 token 给出概率分布。

1. Transformer Decoder-only 的结构

目前主流语言模型（GPT、LLaMA 等）都采用 Decoder-only Transformer，因为该结构天然适合自回归预测。

Transformer的结构有许多变种，现代LLM中常用的decoder-only transformer的一个常见的版本如下图所示：

Architecture of a decoder-only transformer language model.
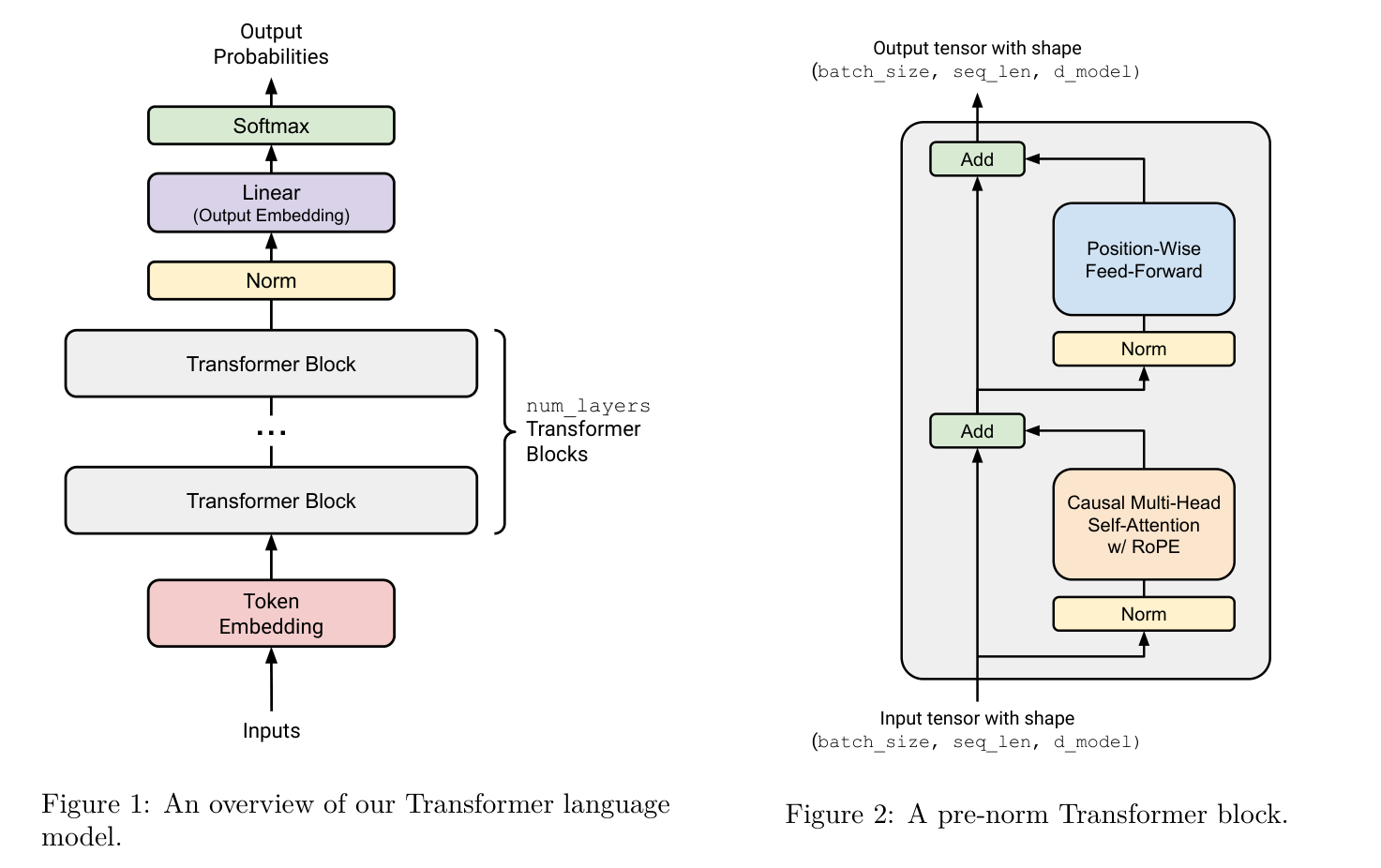
Source of figure: Language Models from Scratch, Stanford CS336 course notes

1.1 输入表示：Token Embedding + Position Embedding

序列的离散 token 首先映射到向量空间：

$$e_t = E[x_t] \in \mathbb{R}^d,$$

其中 $x_t$ 是第 $t$ 个 token 的 id，$E \in \mathbb{R}^{|\mathcal{V}|\times d}$ 是可训练的词嵌入矩阵，$E[x_t]$ 表示取矩阵 $E$ 的第 $x_t$ 行，得到一个 $d$ 维向量 $e_t$。这个过程称为 Token embedding，它将每一个 token 映射为向量。

由于注意力机制本身不编码位置信息，因此加入位置向量 $p_t$（传统的位置编码）：

$$h_t^{(0)} = e_t + p_t.$$

第一层 Transformer 的输入就是

$$H^{(0)} = (h_1^{(0)}, \dots, h_T^{(0)}) \in \mathbb{R}^{T\times d}.$$

2. Transformer Block：Masked Self-Attention + FFN

每一层 Transformer 都包含两部分：

1. Masked Self-Attention（核心）
2. Feed-Forward Network（逐点非线性）

并辅以残差连接（Residual）和 Layer Normalization（LN）。

2.1 Q/K/V 的线性映射：注意力的基础

设当前层的输入为

$$H = (h_1,\dots,h_T) \in \mathbb{R}^{T\times d}.$$

通过三组可训练矩阵映射得到：

$$Q = HW_Q,\quad K = HW_K,\quad V = HW_V.$$

其中 $W_Q, W_K, W_V \in \mathbb{R}^{d \times d}$为可训练的矩阵，他们分别将 $H$ 映射为 $Q,K,V \in \mathbb{R}^{T \times d}$：

• Query $Q$ 表示“我想从别人那里获取什么信息”（我现在想找什么？）
• Key $K$ 表示“我是什么类型的信息”（我身上有什么特征？）
• Value $V$ 表示“我携带的信息内容”（如果你关注我，你能从我这里拿走什么信息？）

$Q$ 和 $K$ 仅仅是用来决定如何从 $V$ 中拿走信息。形象地来说：

$Q$ 和 $K$ 用来“对眼神”，$V$ 才是真正被拿走的信息。

这是注意力机制的基础。

2.2 缩放点积注意力（Scaled Dot-Product Attention）

注意力机制是指我们将 Q 和 K 每个 Token 对应的位置彼此进行相似性比较，然后按照重要性程度决定如何从 $V$ 中提取信息的过程。

(a) 点积

未加 mask 的注意力权重为：

$$S = \frac{QK^\top}{\sqrt{d_k}},$$

这是一个 $T\times T$ 的矩阵，表示任意 token 之间的相似度。

写成分量的形式可能更容易理解：我们用 $Q_i$ 和 $K_j$ 表示 $Q$ 的第 $i$ 行和 $K$ 的第 $j$ 行，那么矩阵 $S$ 的第 $(i,j)$ 位置的元素可以写成

$$s_{i,j} = Q_i \cdot K_j$$

这就是说：

第 i 个位置的问题，和第 j 个位置的特征，有多匹配？

我们把所有点积放在一起，得到的矩阵 $S$ 表示

对于第 i 个位置，我对所有位置 j 的关注倾向

(b) 缩放

为了训练的稳定性，我们将点积的结果除以模型维数的平方根 $\sqrt{d_k}$，这称为“缩放点积”。

为什么要除以 $\sqrt{d_k}$?

当 $d_k$（键向量的维度）很大时，点积 $QK^\top$ 的值可能会很大。原因是：对于独立的 $N(0,1)$ 的随机向量 $q$, $k$，点积的方差大约是 $\operatorname{Var}(q\cdot k) = d_k$（虽然点积的结果不再是正态分布）. 这会造成的后果是：点积的数值更大 → softmax 会输出接近 0 或 1 的极端值 → 梯度消失 → 训练不稳定。

解决办法是：在点积之前除以 $\sqrt{d_k}$ 进行缩放，这样可以保证点积的数值不会因为维度变大而过大，softmax 的梯度更稳定。

(c) 语言模型的特有操作：掩模（mask）

语言模型必须“不能看到未来”，因此加入因果 mask：

$$M_{ij}= \begin{cases} 0, & j\le i,\\ -\infty, & j>i. \end{cases}$$

经过这样的mask以后，每个位置对自己和在自己之前的位置的相关性打分没有变化，但是对自己之后的位置的打分被抹去了（抹去的原因是下一步softmax操作后 $-\infty$ 分数的位置会得到 0 .

自回归的关键点

由于 mask 强制 $A_{ij}=0$（softmax 后趋近 0）对所有 $j > i$， 因此：

Token $t$ 的新表示严格只依赖于 $1,\dots,t$ 的输入。

这正是语言模型的因果性（causality）。

(d) Softmax 注意力

Softmax 函数将“相关性打分”变为“注意力”。点积后的结果只是原始分数，不能直接用。

Softmax 做了什么？

$$a_{i,:} = \text{softmax}(s_{i,:})$$

写成矩阵形式：

$$A = \text{softmax}_2(S)$$

这里的 $\text{softmax}_2$ 用来表示我们是在第二个维度上做 softmax 的。

说人话，这个操作是在说：

对于当前这个 Q_i，我到底应该把多少注意力，分给每个 j？

Softmax 带来三个效果：

1. 变成非负
2. 加起来等于 1
3. 拉开差距（更“偏心”）

上面的描述中，我们并没有把上一步操作中的mask放进来。在 decoder-only 的语言模型中，我们需要使用 Masked 注意力：

$$A = \text{softmax}_2(S + M).$$

(e) 信息提取

我们用 $V_j$ 表示 $V$ 的第 j 行，按照注意力权重提取 $V$ 中的信息，得到输出：

$$output_i = \sum_{j=1}^{T} a_{i,j} \cdot V_j$$

写成矩阵形式，这一步信息提取只是一个矩阵乘法：

$$\text{Attn}(H) = AV.$$

用人话说：

我从 $V$ 的每个位置 j 拿一点信息，拿多少，取决于我有多关注它。

V 才是“内容”，Q 和 K 决定“配额”。

(f) 总结

对于序列中的每一个位置，我先用 Query 去和所有 Key 比一遍，看谁跟我当前关注的内容最相关，然后按这个相关程度，从对应的 Value 中把信息加权汇聚过来。

2.3 多头注意力（Multi-Head Attention）

在实际模型中，上述注意力会重复 $h$ 次（称为注意力头），得到多个子空间的相关性，最终拼接并线性映射：

$$\text{MHA}(H) = \bigoplus_{i=1}^{h} \text{Attn}_i(H) \; W_O.$$

多头注意力可以被看作对注意力矩阵的一种 低秩分解。

多头注意力的核心思想是：

将高维注意力机制分成多个低维子空间，使模型能够同时学习多种不同类型的关系。

Transformer 使用 $h$ 个独立注意力头。 设每个头的维度为 $d_h = d / h$。对第 $i$ 个头，其映射矩阵为：

$$W_Q^{(i)} \in \mathbb{R}^{d \times d_h}, \quad W_K^{(i)} \in \mathbb{R}^{d \times d_h}, \quad W_V^{(i)} \in \mathbb{R}^{d \times d_h}.$$

对输入 $H \in \mathbb{R}^{T \times d}$，第 $i$ 个头的 Q/K/V 为：

$$Q^{(i)} = H W_Q^{(i)},\quad K^{(i)} = H W_K^{(i)},\quad V^{(i)} = H W_V^{(i)}.$$

注意力权重矩阵：

$$A^{(i)} = \text{softmax}\left(\frac{Q^{(i)} (K^{(i)})^\top}{\sqrt{d_h}} + M\right).$$

第 $i$ 个头的输出：

$$\text{head}^{(i)} = A^{(i)} V^{(i)}.$$

拼接所有注意力头

将全部 $h$ 个头拼接：

$$\text{Concat}(\text{head}^{(1)},\dots,\text{head}^{(h)}) \in \mathbb{R}^{T \times (h d_h)} = \mathbb{R}^{T \times d}.$$

再乘输出投影矩阵：

$$\text{MHA}(H) = \big[\text{head}^{(1)} || \dots || \text{head}^{(h)} \big] W_O,$$

其中

$$W_O \in \mathbb{R}^{d \times d}.$$

多头注意力的几个关键数学直觉

(1) 低维子空间的分解

每个注意力头在一个 $d_h$ 维子空间中计算 Q/K/V：

$$d_h = d/h.$$

这相当于将注意力矩阵 $QK^\top$ 分解成多组低秩块：

$$QK^\top = \sum_{i=1}^{h} \left( Q^{(i)} (K^{(i)})^\top \right).$$

从矩阵分解视角看：

多头注意力是一种可学习的、稀疏化的、非共享的分块矩阵分解，提升模型刻画多种相关性的能力。

(2) 多种关系模式的并行建模

不同头学到的内容具有明显分工：

• 某些头捕捉句法（例如动词 → 主语）
• 某些头捕捉语义距离（例如主题相关性）
• 某些头偏向局部依赖

即便没有显式监督，模型也能自发形成多类型信息通路（inductive bias）。

2.4 FFN（前馈网络）：对每个 token 逐点施加非线性

对每个 token 独立应用一个两层 MLP：

$$\text{FFN}(x) = W_2 \,\sigma(W_1 x + b_1) + b_2,$$

典型激活函数为 GELU（Gaussian Error Linear Unit）。

FFN 提供了注意力之外的非线性建模能力，使 Transformer 具备 universal approximation 性质。

2.5 残差连接与 LayerNorm

一个完整的 Transformer 层如下：

1. 注意力子层

   $$\tilde H = H + \text{MHA}(\text{LN}(H)).$$

2. FFN 子层

   $$H' = \tilde H + \text{FFN}(\text{LN}(\tilde H)).$$

这样切分能确保梯度稳定，同时加速收敛。

LayerNorm 是 Transformer 成功的关键。下面是详细数学展开。

2.5.1 Layer Normalization 的数学定义

对每个 token 的隐藏向量

$$x = (x_1,x_2,\dots,x_d) \in \mathbb{R}^d,$$

LayerNorm 在 特征维度（而非 batch 或时间维度）做归一化：

1. Step 1 — 求均值

   $$\mu = \frac{1}{d} \sum_{i=1}^{d} x_i.$$

2. Step 2 — 求方差

   $$\sigma^2 = \frac{1}{d} \sum_{i=1}^{d} (x_i - \mu)^2.$$

3. Step 3 — 归一化

   $$\hat x_i = \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}}.$$

4. Step 4 — 线性缩放和平移（可训练参数）

   $$\text{LN}(x)_i = \gamma_i \hat x_i + \beta_i,$$

   其中 $\gamma, \beta \in \mathbb{R}^d$ 是可训练参数.

   $$$$

2.5.2 为什么 Transformer 使用 LayerNorm 而不是 BatchNorm？

BatchNorm 不适合 Transformer 的两个关键原因：

1. 序列长度可变，batch 上的统计量不稳定

   自注意力需要跨 token 计算，batch size 可能很小，而且不同 token 含义完全不同，用 batch 统计意义不大。

2. 生成任务推理时 batch size 通常为 1

   BatchNorm 会退化，而 LayerNorm 不依赖 batch 统计。

所以 LayerNorm 完全避免了这些问题。

2.5.3 “前置 LN”（Pre-LN）结构为什么更稳定？

现代 Transformer（GPT-2/3/4，LLaMA 系列）几乎全部使用以下结构：

$$\tilde H = H + \text{MHA}(\text{LN}(H)),$$

$$H' = \tilde H + \text{FFN}(\text{LN}(\tilde H)).$$

称为 Pre-LN。

相比旧的 Post-LN：

$$\text{LN}(H + \text{MHA}(H)),$$

Pre-LN 具备显著优势：

1. 梯度路径更短，消除梯度消失

   在 Pre-LN 中，残差路径为：

   $$H \longrightarrow \tilde H$$

   完全绕过了 MHA 和 FFN 内部的复杂操作，使训练深度模型更稳定。

2. 每个子层都接收归一化后的输入，数值更稳定

3. 微分方程视角：有研究表明 Transformer 可被视为数值积分方程的离散化，Pre-LN 对应更稳定的显式方法。

3. Transformer 完成语言建模的数学机制

经过 $L$ 层后得到 final hidden state：

$$h_t^{(L)}.$$

3.1 从隐藏状态到输出概率

使用输出矩阵 $W_{\text{out}}$ 计算 logits：

$$z_t = W_{\text{out}} h_t^{(L)}.$$

然后通过 softmax 得到条件概率：

$$p_\theta(x_t \mid x_{<t}) = \frac{\exp(z_{t, x_t})}{ \sum_{w\in \mathcal{V}} \exp(z_{t, w}) }.$$

3.2 自回归语言模型的训练目标

整个序列的损失为：

$$\mathcal{L}(\theta)= -\sum_{t=1}^T \log p_\theta (x_t \mid x_{<t}).$$

训练输入是完整句子，但 mask 确保模型仍满足自回归因果性。

Teacher forcing 自动成立： 模型每个位置在训练时都能看到完整 prefix。

4. 推理（Inference）：Transformer 如何生成文本

给定前缀 $x_1,\dots,x_{t-1}$，模型预测下一个 token. 主要有两种方式：

1. Greedy （简单）：

$$x_t = \arg\max_{w \in \mathcal{V}} p_\theta(w \mid x_{<t}).$$

2. Random Sampling（Top-k / Top-p / Temperature）（常见）：

$$x_t \sim p_\theta(\cdot \mid x_{<t}).$$

生成过程是逐步执行的，直到生成结束符或达到设定长度。

5. 总结：Transformer LM 的最小数学框架

我们用五步概括 Transformer 如何实现语言建模：

1. 输入嵌入

   $$h_t^{(0)} = E[x_t] + p_t.$$

2. 多层因果自注意力

   $$A=\text{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}+M\right),\quad H\leftarrow AV.$$

3. 深度结构（残差 + LN + FFN）

   自注意力构建上下文依赖，FFN 提供非线性表达。

4. 最大似然训练

   $$\mathcal{L} = -\sum_t \log p_\theta(x_t|x_{<t}).$$

5. 逐步生成

   $$x_t \sim p_\theta(\cdot\mid x_{<t}).$$

一句话总结：

Transformer 语言模型是一种通过多层因果自注意力将前缀压缩为上下文表示，并使用最大似然训练来预测下一个 token 的深度神经网络。